Many fixed income investors are familiar with the concept of duration. It generally represents the change in the value of a bond that results from a 1% change in interest rates. If interest rates go up by 1%, a bond currently priced at par (100) with a duration of 5 will go down in value by 5 to 95. Check out Investor Words for a more detailed discussion.
Before we dig deeper into the application of duration to equities other than bonds, we need to take a brief digression for a quick refresher on asset valuation. In a pure sense, investments are worth the net present value of all of the future cash flows the investment will provide. The net present value is calculated by discounting each of the individual cash flows back to today using some interest rate. If my discount rate (or interest rate) is 5% and I am going to get $100 tomorrow, what is that investment worth to me today? $95.24. Here’s the math: $100/((1.00+5%)^1). So, we can think about duration as the impact of changing the discount rate we use to calculate the net present value of an asset’s future cash flows.
With that background, let’s take a look at how duration applies to equities. Equity investments have a much longer duration than fixed income investments because there is no set date for a return of principal. An equity investment’s dividends could continue to grow and pay ad infinitum. Therefore, equity investments are much more sensitive than fixed income investments to changes in the discount rate (i.e. the interest rate as described above). Within equities, a stock that pays a very high dividend and whose price implies little growth (e.g. Altria, MO) will have a much lower duration than an equity that pays no dividend and whose price implies substantial growth (e.g. Google, GOOG).
As we articulate in our most recent quarterly letter, we believe the current economic environment has the potential to leave corporate earnings volatile for some time and to increase the volatility of inflation, both of which could lead investors to increase their discount rate. So, all things being equal we believe equity investments that pay high dividends compared to those that pay no dividends and whose prices imply very high growth will outperform the overall stock market.
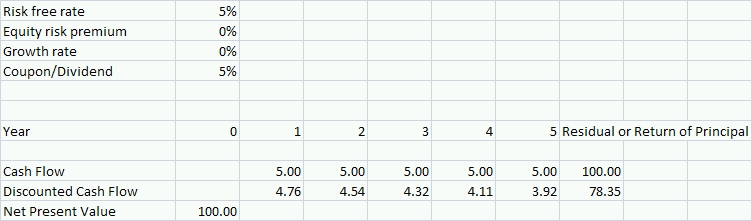
To illustrate why the duration on an equity is much higher than that on a bond, let us look at a couple of examples. First, assume we are talking about a Treasury bond with a 5% coupon and 5 years until the bond matures. Also, assume that the risk-free interest rate is currently 5%. As illustrated in the table below, the net present value of that bond is 100. We get to this value by discounting the bond’s annual coupons and the final return of capital at the risk-free rate.
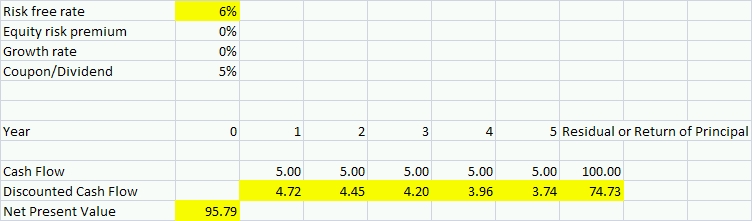
Now suppose we purchase that bond for 100. Immediately, new economic news comes out and the risk-free interest rate moves to 6%. How much is our bond now worth? The answer is 95.79(1). The following table illustrates the changes in the value of the discounted cash flows based on the new 6% discount rate, as opposed to the old 5% discount rate.
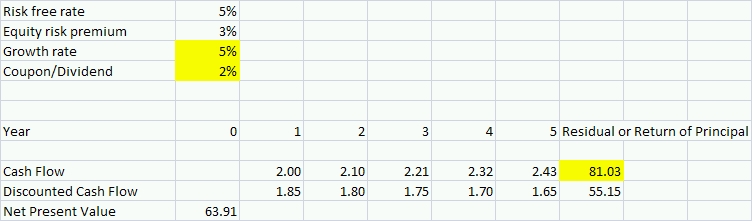
Now that we have seen why a change in interest rates changes the value of a bond, we turn to an example of an equity. Below, we model an equity investment that pays a 2% dividend which we think will grow at 3%. The risk-free rate is back to 5%, but now we add in a 3% equity risk premium. The net present value calculation tells us that an investment with these characteristics is worth 63.91. Notice that the cash flow for the residual value is highlighted. Unlike a bond, an equity investor is not promised a return of principal. The residual value of the equity that exists beyond the 5 year period we have chosen to model is just the present value of the future dividend stream that we can expect a new investor to pay. (The formula for the residual is a perpetuity: dividend/(discount rate – growth rate).)
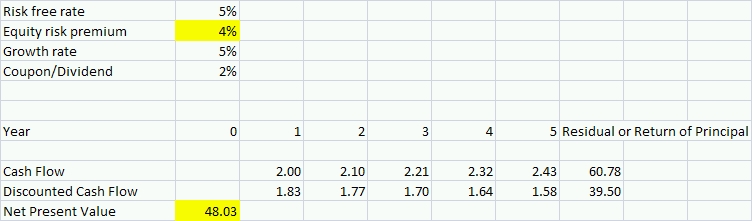
Rather than change the risk-free rate, we increase the equity risk premium in the final example below to demonstrate that an equity investment with these characteristics has a duration of almost 25. A 1% increase in the equity risk premium changes the net present value of the investment to 48.03. (48.03 is 25% below 63.91.) Notice how sensitive the value of an equity investment can be to the discount rate. Valuing an equity investment is a very imprecise process which is why it is important to have a very large margin of safety (i.e. an undervalued asset) before making an investment.
In conclusion, we believe the concept of duration is just as relevant when thinking about equity investments as it is when thinking about interest rate risk and fixed income investments. For a more detailed analysis of the impact inflation has had on the equity risk premium, review Ed Easterling’s work here. For further reading on equity duration, both Ben Inker of GMO and John Hussman of the eponymous Hussman Funds have explored this concept as it applies to the overall stock market. Their analysis is worth reviewing. If you would like to play along at home, you can download the spreadsheet model we used in this analysis here.
1 Careful readers will note that the 1% interest rate increase led to a 4.21% decrease in the value of the bond, NOT a 5% decrease. This is because a 5-year, 5% coupon bond has a duration that is slightly less than 5. A zero-coupon, 5-year bond would have a duration of exactly 5. This is because as an investor receives each coupon, that portion of the value is no longer subject to the new interest rate.